Table of Contents
Thermische Ausdehnung und Dichte
Die thermische Ausdehnung von Materialien kann zu großen wirtschaftlichen Schäden führen. Im Bauwesen müssen zum Beispiel Dehnungsfugen vorgesehen werden, um Längenänderungen bei Temperaturschwankungen auszugleichen. Weiterhin müssen die Ausdehnungskoeffizienten von sich kontaktierenden Materialien aufeinander abgestimmt sein. Unterscheiden sich die Ausdehnungskoeffizienten eines keramischen Körpers und einer Glasur zu stark, so entstehen die sogenannten „spiderweb-cracks“, die häufig auf alten Porzellantellern zu beobachten sind.

Die Ausdehnung findet dabei in allen Raumrichtungen statt, sodass sich die Dichte ändert, da die Masse konstant bleibt. Die Ausdehnung ist bei anisotropen Materialien richtungsabhängig, sodass die Richtung der Ausdehnung angegeben werden muss. Zur Bestimmung der Dichte bzw. des Volumenausdehnungskoeffizienten müssen folglich alle Raumrichtungen beachtet werden.
Definition der thermischen Ausdehnung
Der Längenausdehnungskoeffizient α, auch CTE („coefficient of thermal expansion“) genannt, ist definiert als die relative Längenänderung bei einer Temperaturänderung um ein Kelvin:
α= ∆L/(L0 *∆T)
mit:
∆L: Längenänderung [m]
L0: Ausgangslänge [m]
∆T: Temperaturänderung [K]
ergibt sich für α die Einheit K-1 („pro Kelvin“). Er ist temperaturabhängig, ändert sich also, oft jedoch nur in geringem Masse, abhängig vom betrachteten Temperaturbereich. Seine Größenordnung beträgt typischerweise 10-6 K-1 und wird deshalb häufig in „ppm K-1“ angegeben.
Materialien mit geringen Ausdehnungskoeffizienten sind zum Beispiel Quarzglas und das Metall INVAR, die einen Ausdehnungskoeffizienten kleiner 1 ppm K-1 aufweisen. Die größten Ausdehnungskoeffizienten haben Polymere (bis ca. 200 ppm K-1). Manche Materialien weisen, je nach Temperaturbereich, negative Ausdehnungen auf.
Phasenumwandlungen
Ausdehnungskoeffizienten verschiedener Phasen desselben Materials unterscheiden sich. Zum Beispiel sind die Ausdehnungskoeffizienten von Polymeren oberhalb der Glasübergangstemperatur größer als unterhalb.
Ein weiteres bekanntes Beispiel sind die Phasenumwandlungen von elementarem Eisen: bis 906°C ist die kubisch-raumzentrierte Kristallstruktur stabil (α-Eisen), von 906 °C bis 1401 °C die kubisch-dichteste (β-Eisen) und oberhalb von 1539 °C wieder die kubisch-raumzentrierte (δ-Eisen). Da die Raumerfüllung der kubisch-dichtesten Packung (74 %) größer ist als die der kubisch-raumzentrierten (68 %), finden sich bei den Phasenumwandlungen Sprünge der Dichte und damit auch der Länge. Diese werden benutzt, um Phasenübergänge bei Eisenlegierungen zu detektieren:
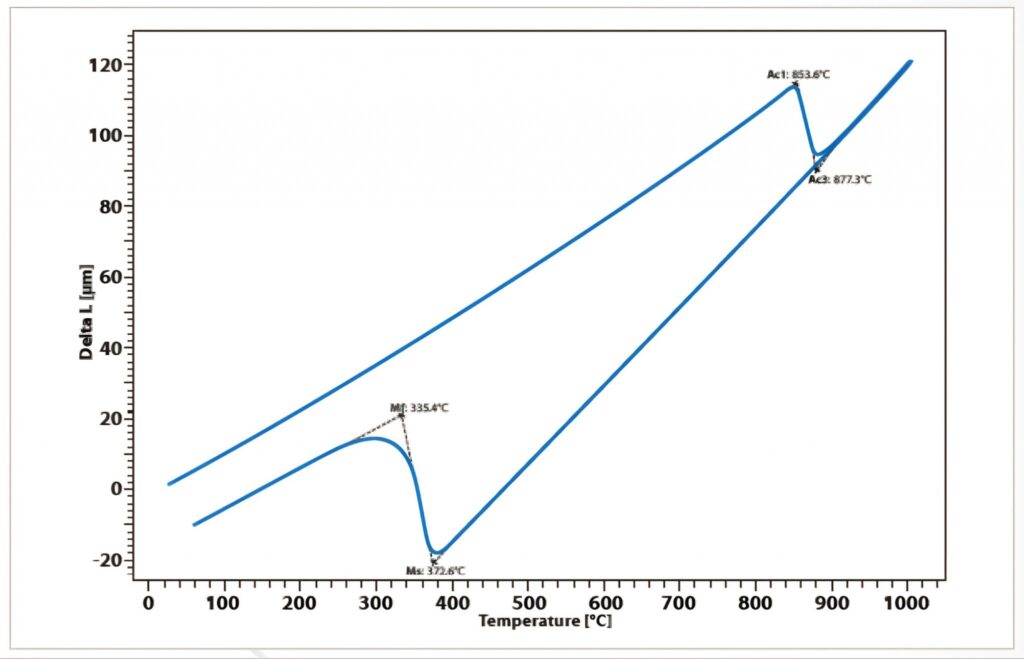
Messung des Ausdehnungskoeffizienten
Flüssigkeiten
Die Ausdehnung bzw. die Dichte von Flüssigkeiten werden im Allgemeinen mit Pyknometern bestimmt. Hierbei wird ein konstantes Volumen der Probe temperiert und die Masse bestimmt. Flüssigkeiten dehnen sich meist mit steigender Temperatur aus. Eine bekannte Ausnahme ist Wasser, das sein Dichtemaximum bei 4 °C hat („Anomalie des Wassers“).
Weiterhin wird die sogenannte Biegeschwing-Methode genutzt. Hierbei wird die Dichte aus der Messung der Eigenfrequenz eines mit der zu untersuchenden Flüssigkeit gefüllten Biegeschwingers errechnet.
Flüssigkeiten können auch mithilfe geeigneter Flüssigkeitscontainern auf einem Schubstangen-Dilatometer vermessen werden. Hierbei ist darauf zu achten, dass keine Gase aus der Flüssigkeit entweichen bzw. entweichende Gase auch den Container verlassen, wobei jedoch die flüssige Probe nicht entweichen darf.
Festkörper
Festkörper werden meist mithilfe von (Schubstangen-)Dilatometern oder thermomechanischen Analysatoren (TMA) vermessen. Hierbei wird die Probe in einen Ofen eingebracht und mit einer Schubstange kontaktiert. Die Längenänderung der Probe wird durch die Schubstange auf einen Sensor übertragen. Je nach verwendetem Ofen kann ein Temperaturbereich von -263 bis +2800 °C abgedeckt werden. Je nach Temperaturbereich werden Schubstangen aus Quarzglas, Aluminiumoxid oder Grafit verwendet. Als Sensoren werden meist Differentialtransformatoren (LVDT – Linear Variable Differential Transformer) und neuerdings auch optische Encoder eingesetzt.
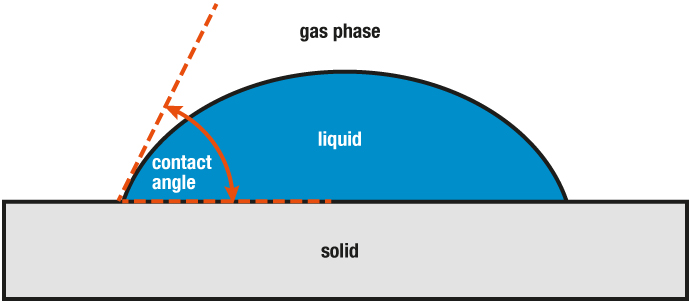
Sind die Proben aufgrund ihrer Eigenschaften schwer zu bearbeiten, zerbrechlich oder leicht verformbar, so dass sie der Kraft der kontaktierenden Schubstange nicht standhalten, werden optische Dilatometer, auch Erhitzungsmikroskop genannt, verwendet. Hier wird, wie im Falle der Schubstangen-Dilatometer, die Probe in einem Ofen platziert. Die Probe wird mit einer Kamera beobachtet, deren Bilder vermessen werden. Durch Bildanalyse können nicht nur die Ausdehnung (hier sogar in 2 Dimensionen) sondern auch Formveränderungen und das Schmelzen beobachtet und Kontaktwinkel berechnet werden.
Pulverförmige Proben werden in speziellen Adaptern vermessen. Hierbei ist darauf zu achten, dass die eingeschlossene Luft, nicht aber die Probe, entweichen kann (analog zur Vermessung von Flüssigkeiten). Auch der Kompaktierungsgrad (Schüttdichte, Rütteldichte, Stampfdichte) der Probe muss beachtet werden: er darf durch die Messbedingungen nicht verändert werden.
Materialien mit besonders geringen Ausdehnungskoeffizienten werden mit interferometrischen Methoden vermessen. Hierbei wird monochromatisches Licht von der Probe reflektiert und mit einem zweiten Strahl zur Interferenz gebracht (Prinzip des Michelson-Interferometers). Die Längenänderung ergibt sich aus Wellenlänge des verwendeten Lichts und der Anzahl der Interferenzen. Solche Messgeräte werden auch LASER-Dilatometer genannt.
