Mesure Van-der-Pauw
Mesure Van-der-Pauw
La méthode de mesure Van der Pauw, nommée d’après son inventeur Leo J. van der Pauw, est largement utilisée comme mesure en 4 points pour déterminer la résistance de la feuille et le coefficient de Hall des matériaux.
En 1958, van der Pauw a résolu le problème général de la distribution du potentiel dans une couche conductrice mince de forme quelconque et a ainsi rendu possible la réalisation de mesures de Hall et de résistance sur ces couches.
Cependant, certaines conditions doivent être remplies pour que la mesure soit correcte.
- L’épaisseur t de l’échantillon doit être homogène et faible par rapport à la distance entre les contacts.
- Il doit être constitué d’une forme continue au sens mathématique du terme et ne doit donc pas comporter de trous ou d’îlots en matériau hautement conducteur.
- Les quatre contacts doivent être situés sur le bord de l’échantillon et être petits par rapport à la surface de l’échantillon.
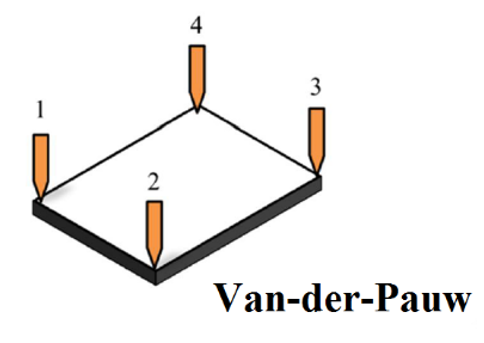
Fig. 1) Dispositif expérimental pour la mesure Van-der-Pauw
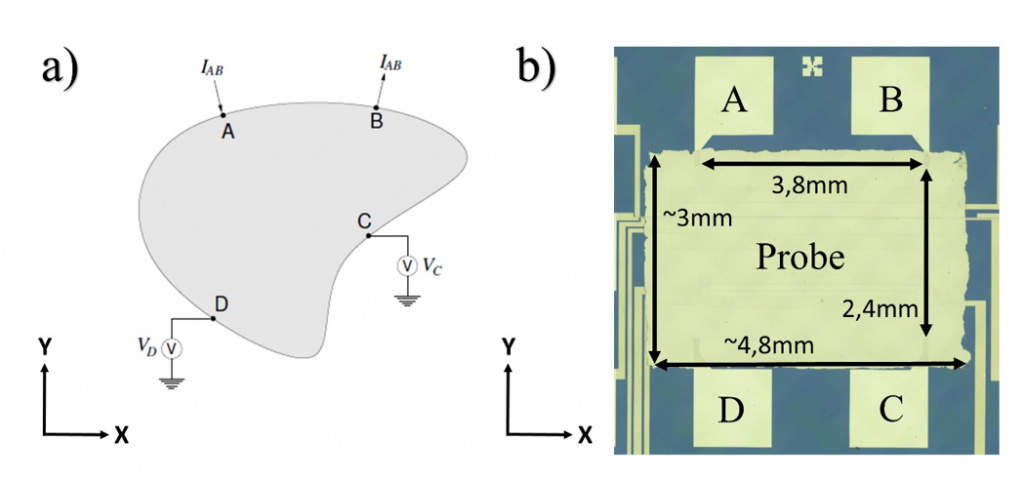
Fig. 2 a) Mise en contact d’un échantillon pour la mesure de Van-der-Pauw. b) Mise en contact de l’échantillon sur la puce de mesure TFA, y compris ses dimensions.
Si toutes les conditions sont remplies, on obtient un échantillon préparé avec les contacts de bord A, B, C et D, comme le montre la figure. 2a-b. Pour calculer la conductivité électrique, il faut mesurer les résistances horizontales et verticales de Van der Pauw R(ij,kl), la mesure de la résistance horizontale s’effectuant comme suit :
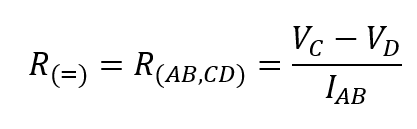
Où VC est la tension du contact mesurée par rapport à la terre et IAB est le courant appliqué entre les contacts A et B, commençant en A et se terminant en B. Si les contacts sont changés cycliquement, la résistance verticale de Van der Pauw peut être déterminée.
Si les résistances horizontale et verticale ont été mesurées, la résistance de surface ou, si l’épaisseur de la couche est connue, la résistivité peut être calculée en résolvant numériquement la formule de Van der Pauw :
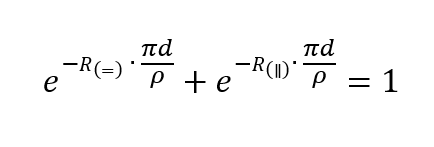
La conductivité électrique étant l’inverse de la résistance spécifique, elle peut être calculée selon l’équation suivante.
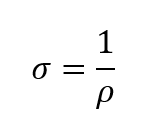
Pour déterminer le coefficient de Hall de l’échantillon, un champ magnétique externe avec une densité de flux BZ peut être appliqué perpendiculairement à la surface de l’échantillon et la variation de la résistance diagonale de Van der Pauw (voir figure 3), en fonction de l’intensité du champ magnétique, est mesurée.
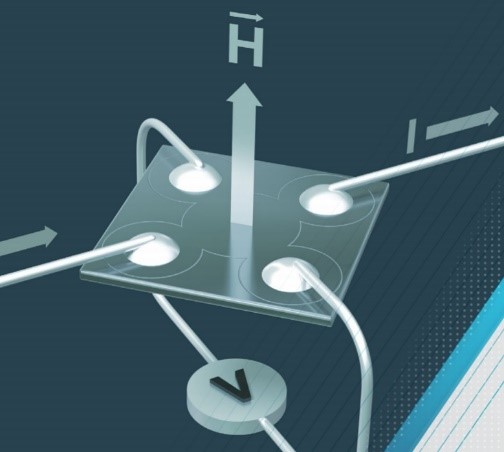
Fig. 3) Configuration de l’échantillon pour la mesure du coefficient de Hall à l’aide de la technologie de mesure Van der Pauw, avec un champ magnétique appliqué perpendiculairement à la surface de l’échantillon.
Dans ce cas, les éléments suivants sont valables :
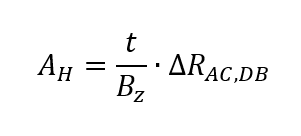
tels que
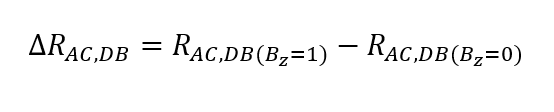
avec le coefficient de HallAH et la densité de flux magnétique BZ. Les effets de décalage dans la mesure du courant et de la tension peuvent être supprimés selon le principe de l’inversion du sens de la mesure. Les effets de décalage provenant de la mesure de l’intensité du champ magnétique sont supprimés en mesurant la tension diagonale VHall à différentes intensités de champ magnétique et en déterminant le coefficient de Hall à partir de la pente de la tension de Hall en fonction de l’intensité du champ magnétique. Le calcul final est effectué selon l’équation suivante :
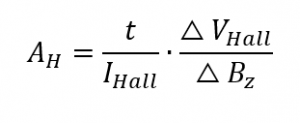
Si la constante de Hall est mesurée à l’aide de la méthode de mesure AC, un champ magnétique alternatif est appliqué et la tension de Hall qui en résulte est lue à l’aide d’un amplificateur lock-in. Il est ainsi possible de mesurer des matériaux dont la mobilité est particulièrement faible, car les tensions de Hall, généralement faibles, ne sont plus superposées par ce que l’on appelle les décalages d’alignement.
Quelles sont les propriétés déterminées ?
La méthode Van-der-Pauw est utilisée pour déterminer les propriétés de transport électrique des matériaux (en vrac et en couches minces) comme la conductivité électrique, la résistivité, la constante de Hall, la concentration de porteurs de charge et la mobilité des porteurs de charge.