3ω Méthode oméga
Technique de mesure 3ω – une approche de la mesure de la conductivité thermique
La méthode 3ω est une approche largement utilisée pour mesurer la conductivité thermique.
Bien qu’initialement développée pour mesurer la conductivité thermique des matériaux en vrac, la méthode a ensuite été étendue à la caractérisation thermique des films minces d’une épaisseur de quelques nm.
En outre, la technique 3ω a été adaptée pour mesurer la conductivité thermique dans le plan et dans le plan transversal de films anisotropes et de membranes autoportantes.
Cette technique est actuellement l’une des méthodes les plus populaires pour la caractérisation de la conductivité thermique des couches minces. caractérisation de la conductivité thermique des couches minces.
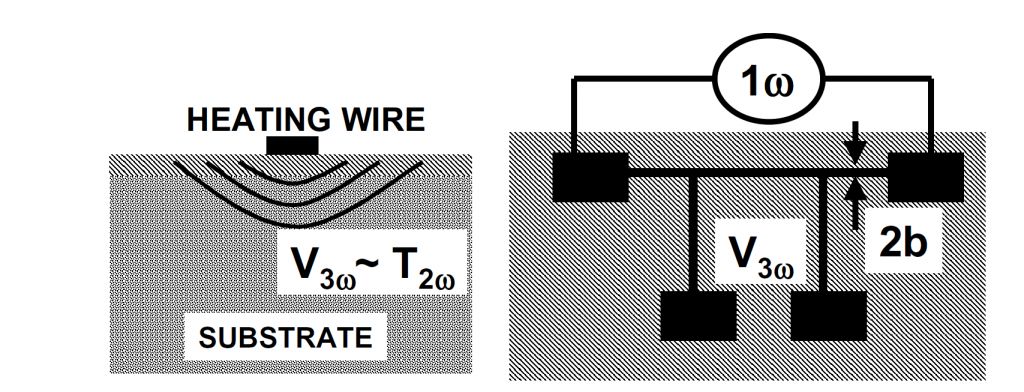Dispositif expérimental (y compris la ligne métallique pour le chauffage et la détection) pour la technique 3 Omega
Dans la méthode 3ω, une fine bande métallique, en contact thermique avec l’échantillon, sert à la fois de chauffage et de capteur de température.
Pour la mesure, un courant alternatif,
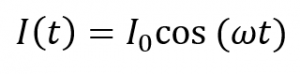
avec une fréquence et une amplitude de modulation angulaire passant à travers la bande, génère une source de chaleur d’une puissance de
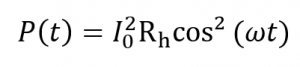
oùRh est la résistance de la bande dans les conditions expérimentales, et provoque une augmentation de la température sous la forme de
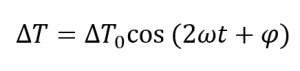
et donc une oscillation de la résistance de la bande
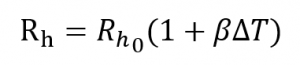
à la fréquence angulaire 2ω, avec est le coefficient de température de la résistance de la bande métallique.
En ce qui concerne la fréquence, le déphasage dépend à la fois de la géométrie de l’élément chauffant et des matériaux sous-jacents.
En mesurant la chute de tension aux bornes de l’élément chauffant, selon la loi d’Ohm, on obtient un signal modulé en amplitude qui présente une petite composante au niveau de la troisième harmonique 3ω, qui peut être extraite à l’aide d’un amplificateur à verrouillage.
Pour calculer la conductivité thermique de l’échantillon ainsi que la capacité thermique spécifique, il faut résoudre l’équation de diffusion de la chaleur correspondante, qui dépend de la configuration expérimentale.
Approche différentielle 3 Oméga avec deux mesures
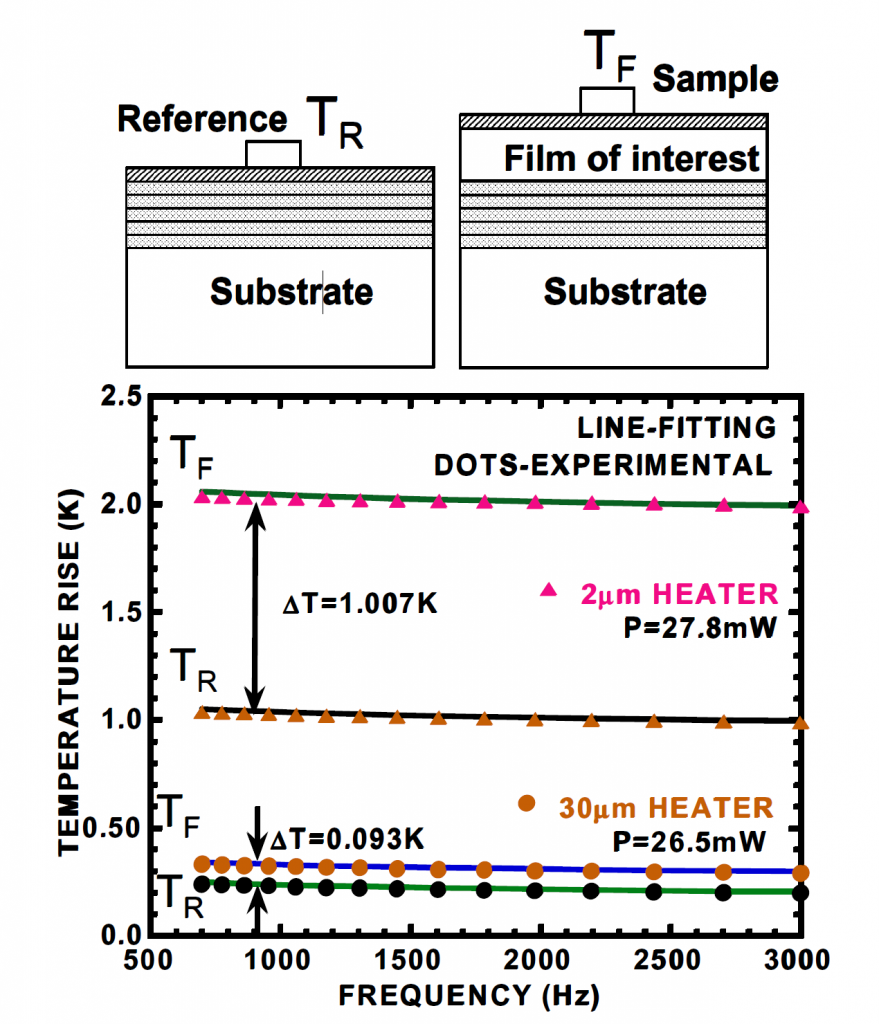
Une approche typique de la conductivité thermique dans le plan transversal avec un film mince sur un substrat en vrac est l’approche différentielle avec deux mesures :
La première concerne uniquement le substrat vierge, et la seconde comprend la couche d’intérêt.
La couche agit comme une résistance thermique connectée en série entre le chauffage et le substrat et assure une augmentation des oscillations de température par rapport à la mesure sans la couche mince.
A partir de cette augmentation, la conductivité thermique de la peut être déterminée à l’aide de la loi de Fourier :
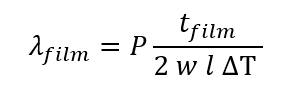
où w et l sont le poids et la longueur de l’appareil de chauffage.
Conductivité thermique dans le plan à l’aide de la technologie de mesure 3ω
Un autre dispositif expérimental permettant de déterminer la conductivité thermique dans le plan ainsi que la capacité thermique spécifique est un dispositif de chauffage aligné au milieu d’une membrane ou d’un substrat suspendu, respectivement. Dans ce cas, le comportement thermique de la partie suspendue peut être évalué à l’aide de la corrélation suivante :
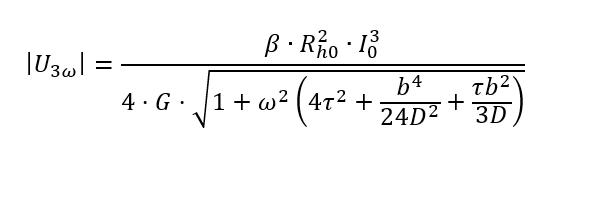
Avec G=2λdlb^(-1), est la constante de temps thermique, b la largeur et l la longueur de la membrane et D la diffusivité thermique.
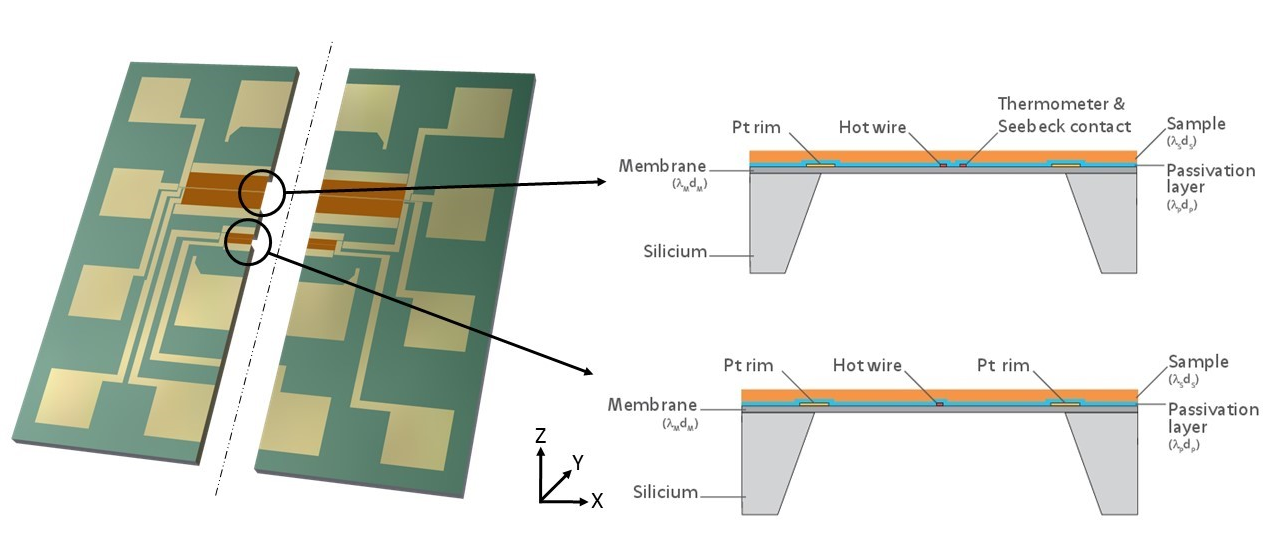Puce de mesure intégrée pour les mesures de conductivité thermique dans le plan de films minces par la méthode 3 Omega
Quelles propriétés seront déterminées ?
La technique de mesure 3ω est une technique de mesure électrothermique permettant de déterminer la conductivité thermique, la diffusivité thermique et la capacité thermique spécifique d’un matériau en vrac (c’est-à-dire solide ou liquide) et de couches minces en utilisant une bande métallique alimentée par un courant alternatif comme élément chauffant.
La résistance métallique appliquée à l’échantillon est chauffée périodiquement.
Les oscillations de température ainsi produites sont ensuite mesurées.
La conductivité thermique et la diffusivité thermique de l’échantillon peuvent être déterminées à partir de leur dépendance à la fréquence.
