Table des matières
Quelle est la résistance thermique de contact ?
La résistance thermique de contact caractérise le transfert de chaleur à l’interface entre deux solides.
En raison des processus de fabrication et d’usinage, mais aussi des propriétés intrinsèques du matériau, la rugosité de la surface est inévitable. Par conséquent, ce n’est pas la totalité de la surface des deux solides qui est en contact direct, mais seulement une fraction, qui n’est donc pas impliquée dans le transport de la chaleur.
Les vides qui en résultent entre les solides sont généralement remplis d’air, un mauvais conducteur de chaleur.[1,2] Il en résulte un saut de température à l’interface.
La résistance thermique spécifique de contact est la suivante :[1]
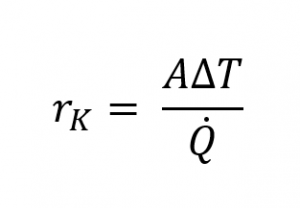
Sa valeur réciproque est également appelée coefficient de contact thermique. Le quotient de la résistance de contact thermique spécifique rk et de la surface de contact macroscopique A est appelé résistance de contact thermique :
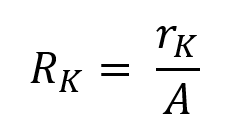
L’unité de résistance thermique de contact est le □(K/W).
Qu'est-ce qui peut influencer la résistance thermique du contact ?
- Rugosité de surface des solides
- Pression de contact sur la surface de contact entre les deux solides
- Remplir les vides entre les surfaces de contact avec de meilleurs matériaux thermoconducteurs, comme par exemple :
- gels, pâtes, matériaux à changement de phase, feuilles, adhésifs, matériaux d’interface thermique, etc.
- En général, la combinaison des deux solides détermine la résistance thermique de contact
Un modèle très simplifié de calcul de la résistance thermique de contact peut être établi à l’aide d’un modèle de résistance. Le flux de chaleur est divisé en composantes solides et fluides et traité séparément. Dans la partie solide, il y a deux résistances connectées en série. La partie qui traverse le fluide est formée par l’air qui y est enfermé. Le transport de la chaleur s’effectue en parallèle à travers les deux canaux, c’est pourquoi il peut être représenté comme un circuit parallèle dans le schéma de circuit équivalent. (cf. figure 1)
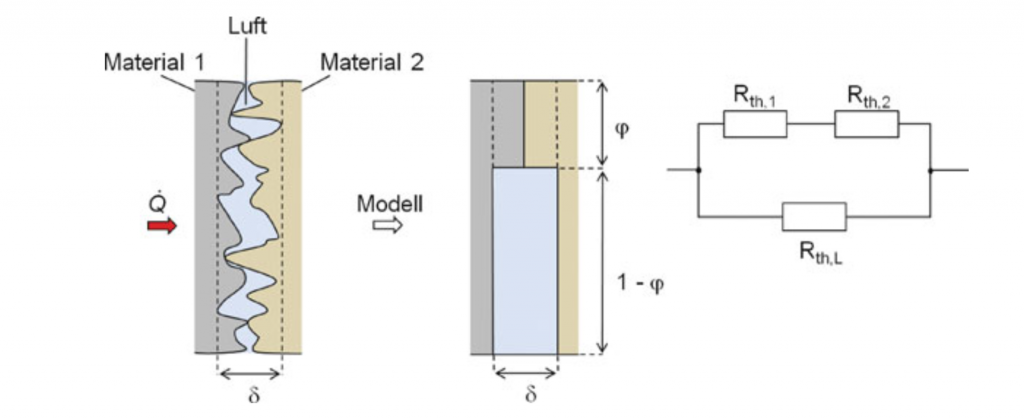
À l’aide du schéma du circuit équivalent et des règles connues pour calculer la résistance en série et en parallèle, on obtient la formule suivante [1] :
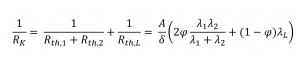
avec
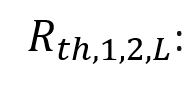
Résistance thermique des matériaux 1,2 ou de l’air en K/W
Elle est valable :
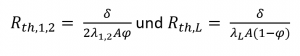
Le modèle présente quelques faiblesses.
Premièrement, il ne prend pas en compte le transfert de chaleur sous forme de rayonnement et deuxièmement, l’épaisseur de la couche limite δ et la partie de la surface nominale qui participe au transfert de chaleur φ ne sont connues que dans les cas les plus rares.
Comment mesurer la résistance thermique du contact ?
La résistance thermique de contact peut être déterminée, par exemple, à l’aide d’un « testeur de matériau d’interface thermique » (testeur TIM).
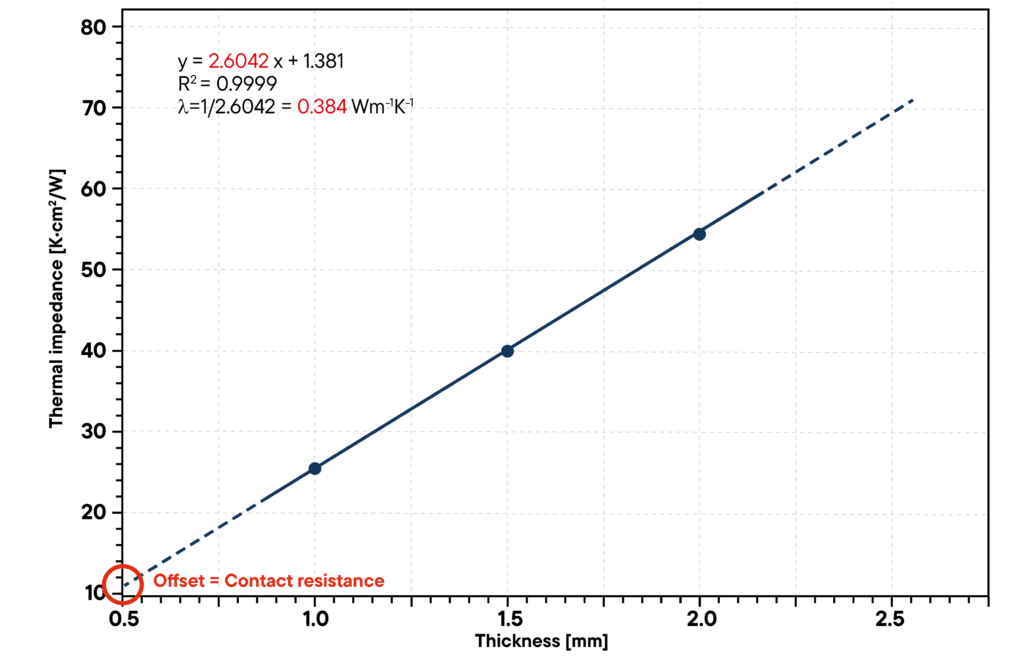
Un testeur TIM mesure l’impédance thermique d’un matériau pour différentes épaisseurs en appliquant un flux de chaleur à travers l’échantillon.
Une ligne droite croissante peut être déterminée à partir des points de mesure via une régression linéaire, et la conductivité thermique peut être déterminée à partir de sa pente.
L’ordonnée de la droite correspond à la résistance thermique de contact entre le matériau et le bloc de mesure.
Par exemple, la barre de mesure peut être en laiton ou en alliage de cuivre ou d’aluminium.
Un exemple d’une telle mesure est illustré à la figure 2.
Il s’agit d’une mesure de l’impédance thermique d’un échantillon de VespelTM d’une taille de 25 mm x 25 mm et d’une pression de contact appliquée de 1 MPa.
Dans cet exemple, des échantillons d’une épaisseur comprise entre 1,1 mm et 3,08 mm ont été mesurés.
Littérature :
[1] Griesinger, Andreas. Wärmemanagement in der Elektronik, Springer Berlin Heidelberg, 2019.
[2] Incropera, DeWitt, Bergmann, Lavine, Fundamentals of heat and mass transfer.pdf », John Wiley & Sons, 2017.