La mobilité des porteurs de charge dans les matériaux semi-conducteurs est un paramètre important pour l’utilisation des cellules solaires. La lumière qui tombe sur une cellule solaire génère des porteurs de charge libres qui produisent une tension électrique sur les électrodes. La mobilité des porteurs de charge dans le matériau détermine le flux de courant dans la cellule et influence donc son rendement utilisable.
Les semi-conducteurs utilisés dans les systèmes photovoltaïques présentent naturellement une faible mobilité ; pour le silicium polycristallin des cellules solaires, elle est de 1 000 à 10 000 fois inférieure à celle du silicium de haute pureté, nécessaire à la fabrication des composants.
La mobilité des porteurs de charge dans les semi-conducteurs peut être mesurée à l’aide de l’effet Hall, conformément à la norme ASTM F76-08. Le type (électrons ou trous) et la densité des porteurs de charge ainsi que leur mobilité dans le matériau peuvent être déterminés par une mesure de la résistance. Bien que la mesure dans un champ magnétique constant (DC) soit très répandue, elle n’est pas adaptée à la mesure précise des matériaux à faible mobilité, tels que ceux utilisés dans la technologie des cellules solaires, la thermoélectricité ou l’électronique organique.
Effet Hall et mesures
Edwin Herbert Hall a découvert l’effet Hall, qui porte son nom, en 1879. Il a observé que le courant dans un conducteur peut être influencé par un champ magnétique externe.
Si un conducteur (semi) porteur de courant est traversé perpendiculairement par un champ magnétique, la force de Lorentz provoque une composante de force qui agit perpendiculairement à la direction du mouvement de la charge, de sorte que les porteurs de charge sont déviés sur une trajectoire circulaire. Cela crée un gradient de concentration des porteurs de charge à l’intérieur du conducteur dans le sens du courant. Il y a un manque d’électrons d’un côté du conducteur et une accumulation de porteurs de charge du côté opposé. La tension qui en résulte est appelée tension de Hall UH. Elle dépend de l’intensité du courant I, de la densité du flux magnétique B, de l’épaisseur de l’échantillon d et d’une constante du matériau, le coefficient de Hall AH.
Équation 1 :
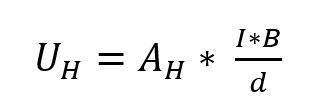
Si le coefficient de Hall a une valeur positive, il s’agit d’un « conducteur à trous » (type p) ; dans la plupart des cas, une valeur négative signifie un conducteur à électrons (type n).
Les équations 2 et 3 montrent d’autres relations entre le coefficient de Hall AH, la résistance spécifique ρ, la densité de porteurs de charge n et la mobilité μ, où e est la charge élémentaire.
Équation 2 :
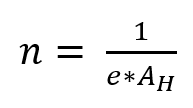
Équation 3 :
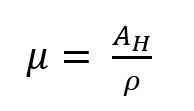
Dans des conditions d’essai réelles, la tension de Hall mesurée UHm peut être influencée par une composante de tension de décalage UO et une composante de tension thermoélectrique Uth.
Une méthode spéciale a été mise au point pour éliminer les effets perturbateurs des tensions UO et Uth.
La tension thermique peut être éliminée en changeant la direction du courant et en calculant la moyenne des valeurs absolues.
La tension de décalage résulte de la géométrie de l’échantillon ; elle peut être compensée en inversant le champ magnétique, car elle ne dépend pas de la direction du champ.
Étant donné que la méthode DC conduit souvent à une détermination incorrecte du type de porteur de charge et à des résultats imprécis pour la mobilité des matériaux à faible mobilité, un champ magnétique alternatif ou un courant alternatif peut être utilisé à la place.
En effet, alors que la tension de Hall devient une tension alternative, les composantes de tension continue UO et Uth peuvent être supprimées.
Les petites tensions de Hall peuvent être mesurées et les matériaux à faible mobilité des porteurs de charge peuvent être caractérisés, de sorte que les matériaux photovoltaïques, en particulier, peuvent être évalués à l’aide de la méthode CA.