« La capacité thermique spécifique indique la capacité d’une substance à stocker la chaleur. Cette quantité de substance correspond à la quantité de chaleur nécessaire pour chauffer une quantité donnée d’une substance à un Kelvin ».
Avec l’aide des DSCs la capacité thermique spécifique (ci-après dénommée Cp) peut être déterminée [3, section 6.2].
La capacité calorifique spécifique, en ajoutant la masse, est une quantité intensive.
Elle indique la quantité de chaleur qu’une substance doit absorber pour augmenter la masse d’une substance par une différence de température définie.
La Cp dépend de la température et se calcule comme suit
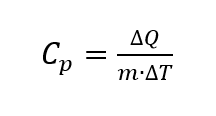
où la pression ambiante est supposée constante [2, p. 118]. L’unité de la capacité thermique spécifique [3, p. 78] est la suivante
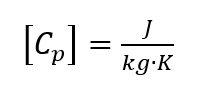
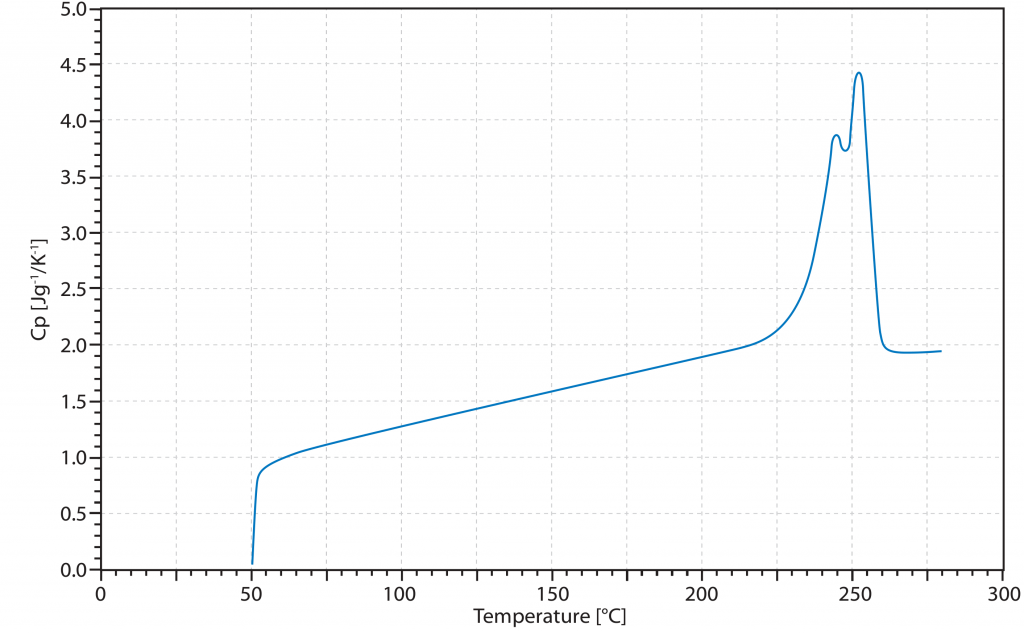
L’augmentation de la valeur Cp indiquée s’explique par le caractère endothermique de cette transition. Le système de mesure doit donc fournir plus d’énergie pour suivre le profil de température donné. Cependant, cela ne correspond pas au Cp réel et c’est pourquoi la capacité thermique spécifique dans la région d’une transition de phase est supposée infinie.
Référencement à l'aide de saphir
Méthodes de détermination de la capacité thermique spécifique par DSC
Il existe plusieurs méthodes pour déterminer la capacité thermique spécifique à l’aide de calorimètres à balayage différentiel. Elles sont brièvement présentées ci-dessous.
Mesure classique de la PC à l'aide de la DSC
La détermination classique de la capacité calorifique spécifique au moyen de DSC s’effectue en trois étapes. Dans un premier temps, seul le creuset de l’échantillon correspondant est chauffé et la courbe zéro correspondant à l’expérience est enregistrée afin de compenser l’inertie du système de mesure. Dans une deuxième étape, un matériau de référence connu est mesuré dans les mêmes conditions expérimentales. La condition préalable est que le matériau soit très pur, bien défini et inerte dans la plage de température souhaitée. De même, les valeurs bibliographiques de la capacité thermique du matériau de référence en fonction de la température doivent être disponibles. Dans une troisième étape, l’échantillon à étudier est mesuré dans les mêmes conditions expérimentales. La courbe zéro est soustraite dans chaque cas des mesures de référence et de l’échantillon. À partir de la différence entre les deux courbes DSC, un facteur d’étalonnage et la comparaison des flux de chaleur permettent de déterminer la capacité calorifique spécifique selon la formule suivante
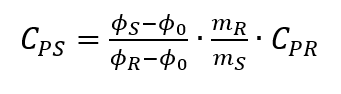
[4, p. 119]. Une illustration des trois courbes et de la méthode est présentée dans la Fig. 2.
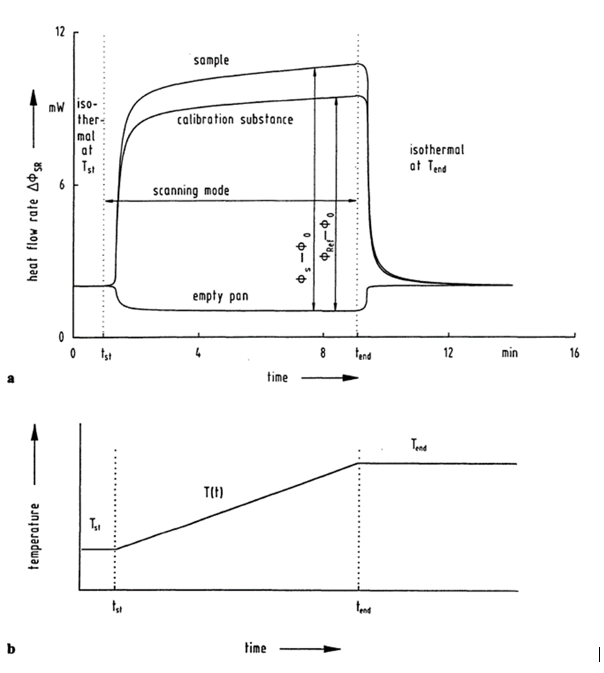
Étant donné que les poids des échantillons sont très faibles, il est nécessaire de déterminer les masses du matériau de référence et de l’échantillon avec une grande précision. Les creusets et toutes les autres conditions ambiantes doivent être maintenus aussi identiques que possible. Dans le cas contraire, des écarts de mesure se produiront, il faut donc veiller à positionner le creuset et l’échantillon avec précision. Le matériau de référence doit également être similaire à l’échantillon étudié en termes de poids initial et de capacité thermique spécifique afin de minimiser les influences telles que les gradients de température à travers l’échantillon.
Mesure de la PC modulée en fonction de la température à l'aide de la DSC
Lors de la détermination de la capacité calorifique spécifique au moyen d’une mesure modulée en température, la courbe de température est superposée à une onde sinusoïdale. Une condition préalable à cette méthode de mesure est que le DSC puisse suivre la température modulée donnée. En conséquence, le profil de température [4, p. 132] peut être décrit comme suit :
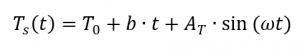
A partir de là, le flux de chaleur résulte de
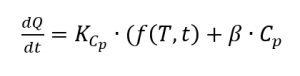
avec
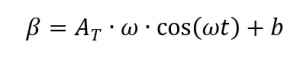
[2, p. 187] qui s’applique
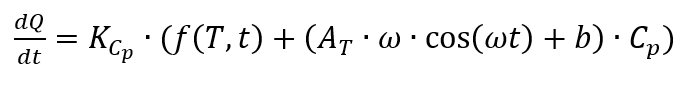
Si la DSC mesurée est évaluée, la capacité thermique spécifique [1, p. 363] est calculée selon la formule suivante
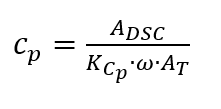
l’inertie des systèmes de mesure et des fours limite l’amplitude et entraîne des périodes longues.
Pour obtenir une bonne résolution de la capacité thermique résultante, il faut passer par un nombre suffisamment important de périodes de modulation, ce qui signifie que les mesures prennent du temps.
Mesure de la PC modulée en fonction de la température à l'aide de la DSC
Lors de la détermination de la capacité calorifique spécifique au moyen d’une mesure modulée en température, la courbe de température est superposée à une onde sinusoïdale. Une condition préalable à cette méthode de mesure est que le DSC puisse suivre la température modulée donnée. Par conséquent, le profil de température [4, p. 132] peut être décrit comme suit :
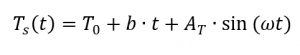
A partir de là, le flux de chaleur résulte de
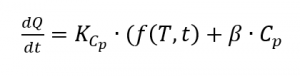
avec
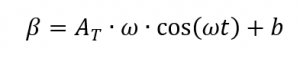
[2, p. 187] qui s’applique
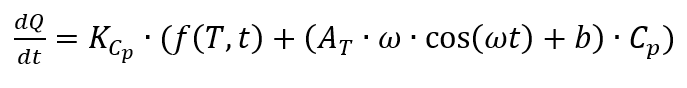
Si le DSC mesuré est évalué, la capacité thermique spécifique [1, p. 363] est calculée selon la formule suivante
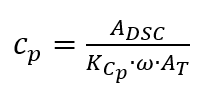
l’inertie des systèmes de mesure et des fours limite l’amplitude et entraîne des périodes longues. Pour obtenir une bonne résolution de la capacité thermique résultante, il faut passer par un nombre suffisamment important de périodes de modulation, ce qui signifie que les mesures prennent du temps.
Séparation des parties réversibles et irréversibles du signal DSC
Un signal DSC peut être divisé en une partie réversible (abrégée en REV dans ce qui suit) et une partie non réversible (abrégée en NONREV dans ce qui suit) selon les critères suivants
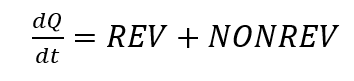
[5, p. 172]. La partie réversible d’un signal DSC comprend les effets qui se produisent de manière reproductible, tels que les transitions vitreuses ou les processus de fusion [2, chap. 3.1.4]. Les effets irréversibles sont ceux qui ne se produisent qu’une seule fois dans l’échantillon correspondant, comme l’évaporation de l’eau. La mesure modulée en température permet de séparer ces signaux les uns des autres. Selon la formule de calcul de la mesure modulée en température [5, p. 172], on peut supposer que
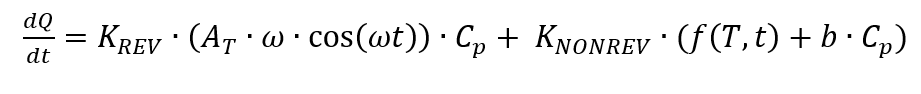
En conséquence, la partie réversible peut être décrite comme suit.
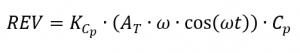
et la partie irréversible d’un signal DSC selon
Si le signal de mesure modulé a été enregistré et que la capacité thermique spécifique a été calculée au moyen de la DSC comme dans le cas de la mesure de la PC modulée en température, la NONREV peut être calculée comme suit
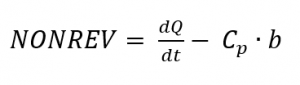
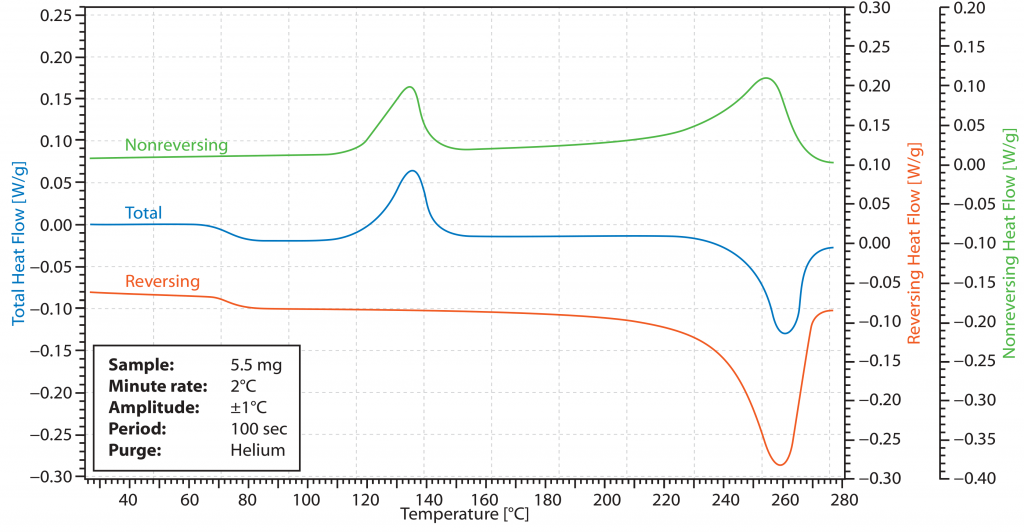
et donc REV peut également être calculé en soustrayant NONREV du signal DSC. Si des effets sont superposés par d’autres pendant les mesures, ils peuvent souvent être clairement attribués et évalués à l’aide de cette séparation. Cependant, le temps et les efforts nécessaires sont nettement plus importants. La Fig. 3 montre une représentation typique d’un signal DSC avec les composantes réversibles et irréversibles associées.
Mesure du 3-Omega CP par DSC
Une autre méthode pour déterminer la capacité thermique spécifique est la méthode 3ω. Inventée par David Cahill, cette méthode utilise un radiateur excité avec une vitesse angulaire ω. La méthode est en fait utilisée pour déterminer la conductivité thermique [6, p. 19]. Celle-ci est déterminée par
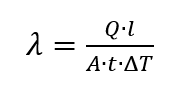
et peut être utilisé en conjonction avec
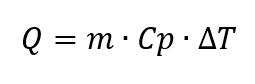
peut être convertie [6, p. 69]. Ainsi, en mesurant le changement de température périodique sur l’échantillon, il est possible de déterminer l’importance de la capacité thermique spécifique. Cependant, étant donné que la méthode est conçue pour mesurer des échantillons à couches minces, qui sont rarement utilisés dans les mesures DSC conventionnelles, la méthode est difficilement adaptée aux instruments DSC conventionnels.
Vous pouvez déterminer la capacité thermique spécifique avec les instruments de mesure Linseis suivants : Chip-DSC, DSC PT 1600, STA
Littérature :
- B. Wunderlich, Analyse thermique des matériaux polymères. Berlin, Heidelberg : Springer-Verlag Berlin Heidelberg, 2005.
- S. M. Sarge, G. W. H. Höhne et W. Hemminger, Calorimetry : Fundamentals, instrumentation and applications. Weinheim, Allemagne : Wiley-VCH Verlag, 2014.
- G. W. H. Höhne, W. Hemminger et H.-J. Flammersheim, Differential Scanning Calorimetry : Une introduction pour les praticiens. Berlin, Heidelberg : Springer, 1996.
- G. W. H. Höhne, W. F. Hemminger und H.-J. Flammersheim, Differential Scanning Calorimetry, 2. Aufl. Berlin, Heidelberg : Springer, 2003.
J. D. Menczel et R. B. Prime, Thermal analysis of polymers. Hoboken, N.J : John Wiley, 2009. - P. Böckh et T. Wetzel, Wärmeübertragung : Grundlagen und Praxis, 5. Aufl. Berlin : Springer Vieweg, 2014.
