Table des matières
Qu'est-ce qu'un matériau thermoélectrique ?
Les matériaux thermoélectriques peuvent convertir directement la chaleur en énergie électrique.
Cette propriété est basée sur l’effet effet Seebeck dans lequel une différence de température appliquée à un matériau génère une tension.
L’inverse est l’effet Peltier, qui est généralement utilisé pour le refroidissement.
Un troisième effet thermoélectrique est l’effet Thomson, qui décrit le transport de chaleur le long d’un conducteur de courant dans lequel existe un gradient de température.
En raison de la possibilité d’utiliser directement l’énergie thermique, les matériaux thermoélectriques sont devenus le centre de la recherche et du développement.
D’une part, ils peuvent être utilisés pour produire de l’énergie électrique à partir de sources d’énergie primaire ; d’autre part, il est tentant de produire de l’électricité à partir de la chaleur résiduelle, ce qui permet de préserver les ressources en combustibles fossiles tout en réduisant les émissions de CO2.
La tension électrique induite par l’effet Seebeck étant très faible (généralement de quelques μV/K à quelques centaines), de grands efforts sont déployés pour développer des matériaux thermoélectriques améliorés.
Les matériaux thermoélectriques classiques appartiennent au groupe des semi-métaux et des semi-conducteurs (groupe principal IV à VI du tableau périodique) ou sont des alliages de matériaux de ces groupes, car le coefficient Seebeck y est particulièrement élevé.
L’effet Seebeck peut être encore augmenté par le dopage.
Qu'est-ce que le chiffre de mérite ?
En général, un chiffre de mérite est une mesure de l’adéquation des matériaux, des méthodes ou des équipements par rapport à d’autres solutions.
Le facteur de mérite thermoélectrique thermoélectrique « ZT » décrit l’adéquation des matériaux thermoélectriques et est défini comme suit :
Équation 1
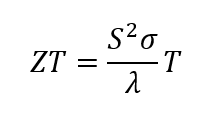
Les matériaux thermoélectriques doivent avoir une faible conductivité thermique et une une conductivité électrique élevée en plus d’un coefficient Seebeck aussi élevé que possible.
Les matériaux à forte conductivité thermique ne permettent pas de grands gradients de température ; si la conductivité électrique est faible, aucun courant utile ne peut être obtenu.
En outre, le facteur de mérite et la différence de température sont directement liés à l’efficacité η d’un dispositif thermoélectrique, qui augmente donc lorsque ZT et ΔT ont des valeurs élevées.
Équation 2
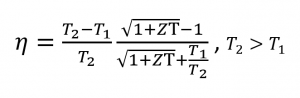
Optimisation des matériaux thermoélectriques
Une grande variété de classes de matériaux présente des effets thermoélectriques de différentes intensités.
Pendant longtemps, une valeur de 1 était considérée comme le chiffre de mérite maximal, mais aujourd’hui, certains matériaux optimisés atteignent des valeurs de l’ordre de 2 ou plus.
Comme le montre l’équation 1, il existe deux approches différentes pour augmenter ZT : soit le facteur de puissance S2σ peut être maximisé, et/ou le facteur de puissance S2σ peut être maximisé, et/ou le facteur de puissance S2σ peut être maximisé, et/ou le facteur de puissance S2σ peut être maximisé. conductivité thermique peut être minimisée.
Pour ce faire, les matériaux existants sont améliorés, par exemple par dopage, et de nouveaux matériaux sont développés.
Ce dernier objectif peut être atteint, par exemple, par la nanostructuration, qui permet de réduire considérablement la conductivité thermique sans influencer fortement le facteur de puissance.
Si les thermoélectriques sont utilisés dans l’industrie, le coût, la toxicité et la disponibilité des matériaux sont des considérations essentielles.
Mesure du facteur de mérite
Il existe plusieurs méthodes pour déterminer le facteur de mérite thermoélectrique.
- Tout d’abord, les paramètres individuels (coefficient Seebeck, conductivité électrique et thermique) peuvent être mesurés et le ZT calculé selon l’équation 1.
- En revanche, il est possible de déterminer ZT directement à l’aide de la méthode Harman.
1. Calcul de l'équation 1
Différents appareils commerciaux sont disponibles pour mesurer quasi-simultanément la conductivité électrique et le coefficient Seebeck.
La conductivité thermique est généralement déterminée par la méthode du laser ou du flash lumineux.
Le résultat direct de cette méthode est la diffusivité thermique.
Si vous connaissez la densité et la capacité thermique spécifique.
La conductivité thermique peut être calculée à partir de la formule suivante :
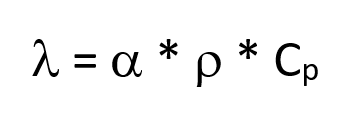
Toutes ces variables dépendent de la température
Par conséquent, un total de cinq variables (dépendant de la température) doit être déterminé afin de calculer le facteur de mérite. Une analyse d’erreur peut être trouvée dans la littérature [1].
2. Détermination par la méthode Harman
La méthode Harman permet de mesurer directement le facteur de mérite. Pour ce faire, on fait passer un petit courant à travers un échantillon en forme de tige dans des conditions adiabatiques. La chute de tension observée est composée d’une composante ohmique (UR; résistance électrique) et d’une composante thermoélectrique causée par l’effet Seebeck (Uth; tension thermique). Contrairement à la composante ohmique, qui se produit spontanément, celle causée par l’effet Seebeck s’accumule lentement :
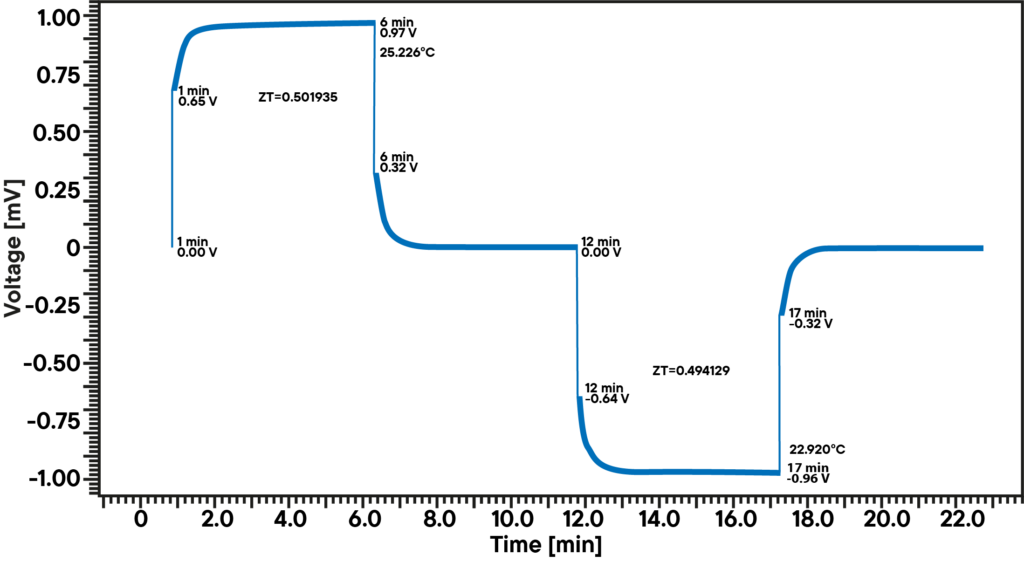
Le chiffre de mérite est obtenu en divisant les deux composantes :
Équation 4
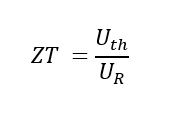
Littérature :
[1] A. Alleno et al, A round robin test of the uncertainty on the measurement.of the thermoelectric dimensionless figure of merit of Co0.97Ni0.03Sb3, REVIEW OF SCIENTIFIC INSTRUMENTS 86, 011301 (2015).
[2] T.C. Harman, Journal of Applied Physics 29, 1373 (1958).
[3] T. C. Harman, J. H. Cahn et M. J. Logan, J. Appl. Phys. 30(9), 1351 (1959).
